Diffusion-LLMs

Just thinking like what diffusion model do in pure image generation

• Masking paradigm 1: Absorbing-state Discrete Diffusion Models The core principle is simple:

  1. Take a piece of perfect data (like a sentence).
  2. Systematically and slowly destroy it by adding “noise” until it’s unrecognizable.
  3. Train the model to learn how to precisely reverse that destruction process.

  How to corrupt a discrete token? We have one additional ‘[MASK]’ token, which is used to replace the corrupted token.

  \begin{equation} q(x_t | \mathbf{x}) = \text{Cat}(\alpha_t \mathbf{x} + (1 - \alpha_t)\mathbf{m}) \end{equation}

  Where $\mathbf{x}$ is a one-hot vector of the original token, $\mathbf{m}$ is a one-hot vector of the masked token, and $\alpha_t$ is a scalar that controls the amount of noise added. $\alpha_t$ is a schedular that controls the amount of noise added at each step.

  Then how do we reverse(denoise) the corrupted token?

  \begin{equation} q(x_s | x_t, \mathbf{x}) = \begin{cases} \text{Cat}(x_s | x_t), & \text{if } x_t \neq \mathbf{m} \\ \text{Cat}\left(x_s \left| \frac{(\alpha_s - \alpha_t)\mathbf{x} + (1 - \alpha_s)\mathbf{m}}{1 - \alpha_t}\right.\right), & \text{if } x_t = \mathbf{m} \end{cases} \end{equation}

  Training Objactive: ELBO \begin{equation} \mathcal{L}_{MDM} = -\log p_\theta(x) \leq \int_0^1 \frac{1}{t} \mathbb{E}_{q_{t|0}(x_t | x_0)} \left[ \sum_{i:x_0^i = [MASK] -\log p_\theta(x_0^i|x_t)} \right] dt \end{equation}

  Deduction: Original DDPM: \begin{align} -\log p_\theta(x_0) = -\log\int p_\theta(x_{0:1}) dx_1 \notag\ \le \mathbb{E}_{q} \Bigl[ \log q(x_{0:1}\mid x_0) - \log p_\theta(x_{0:1}) \Bigr] &= \mathcal{L}_{\text{DDPM}} \\ = \mathrm{KL}\bigl(q(x_T \mid x_0)\|p_\theta(x_T)\bigr) + \sum_{t=1}^{T} \mathbb{E}_{q} \Bigl[ \mathrm{KL}\bigl( q(x_{t-1} \mid x_t,x_0)\|_\theta(x_{t-1}\mid x_t) \bigr) \Bigr] \end{align}

  As for discrete diffusion ELBO(Catogorical distribution) at time t, ONLY unmasked token $x_t^i$ can be masked at $dt$ for a position $i$: (e.g. the schedular function $\alpha_t$) \begin{equation} \text{maskrate}(t) = 1-\alpha_t \end{equation}

  So we need to make the mask rate increase $m(t+dt)-m(t)$ during a small time period $dt$: \begin{align} \alpha_t \frac{\text{maskrate}(t+dt) - \text{maskrate}(t)}{\alpha_t} = \text{maskrate}(t+dt) - \text{maskrate}(t) \\ p_{mask} = \frac{\text{maskrate}(t+dt) - \text{maskrate}(t)}{\alpha_t} \\ q_{(t+dt)|t}(x_t^i \to [MASK]) = p_{mask} = \frac{-d\alpha_t}{\alpha_t} ,\quad \text{if } x_t^i \neq [MASK] \end{align}

  Now, reformulate the KL divergence: \begin{align} -\log p_\theta(x_0) \le \mathbb{E}_{q}\Bigl[\log q(x_{0:1} \mid x_0) - \log p_\theta(x_{0:1})\Bigr] = \int_{0}^{1} \underbrace{ \mathbb{E}_{q_{t \mid 0}(x_t \mid x_0)} \Bigl[ \mathrm{KL}\bigl(q_{t+dt \mid t}(\cdot\mid x_t)\|p_\theta(\cdot\mid x_t)\bigr) \Bigr] } \\ \text{where} \quad \mathrm{KL}\bigl(q_{t+dt \mid t}(\cdot\mid x_t)\|p_\theta(\cdot\mid x_t)\bigr) = \sum_{i:x_t^i \neq [\text{MASK}]} q_{t+dt \mid t}(x_t^i \to [MASK])\bigl[ -\log p_\theta(x_0^i \mid x_t) \bigr] \notag\\ = \sum_{i:x_t^i \neq [\text{MASK}]} \bigl( \frac{-d\alpha_t}{\alpha_t} \bigr) \bigl[ -\log p_\theta(x_0^i \mid x_t) \bigr] \notag\\ = -\frac{d\alpha_t}{\alpha_t} \sum_{i:x_t^i \neq [\text{MASK}]} \bigl[ -\log p_\theta(x_0^i \mid x_t) \bigr] \end{align}

  This gives us our final objective, which connects back to Equation (3): \begin{equation} \mathcal{L}_{\text{MDM}} \le \int_0^1 \frac{-d\alpha_t}{\alpha_t} \mathbb{E}{q_{t|0}(x_t | x_0)} \left[ \sum_{i:x_t^i \neq [\text{MASK}]} [-\log p_\theta(x_0^i|x_t)] \right] \end{equation}

• Decoding Paradigm 1: Confidence-based Remasking

  • The core idea is to use a confidence score to determine whether to remask a token during decoding.
  • If the confidence score of a token is below a certain threshold, it is remasked and decoded again.

• Decoding Paradigm 2: Semi-Autoregressive Decoding

  • The core idea is to split response $\mathbf{r}$ into k blocks $\mathbf{r}_1, \mathbf{r}_2, \ldots, \mathbf{r}_k$ and decode each block in an autoregressive way.
  • Inside each block, the model can decode tokens in parallel.

Unified Discrete Diffusion Family

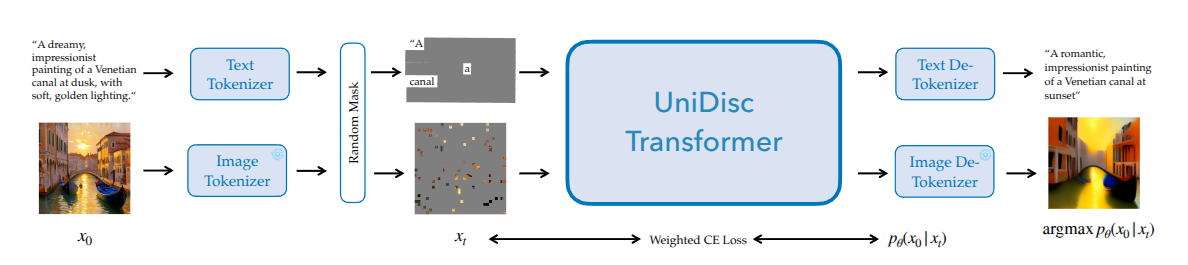
UniDisc: Unified Multimodal Discrete Diffusion

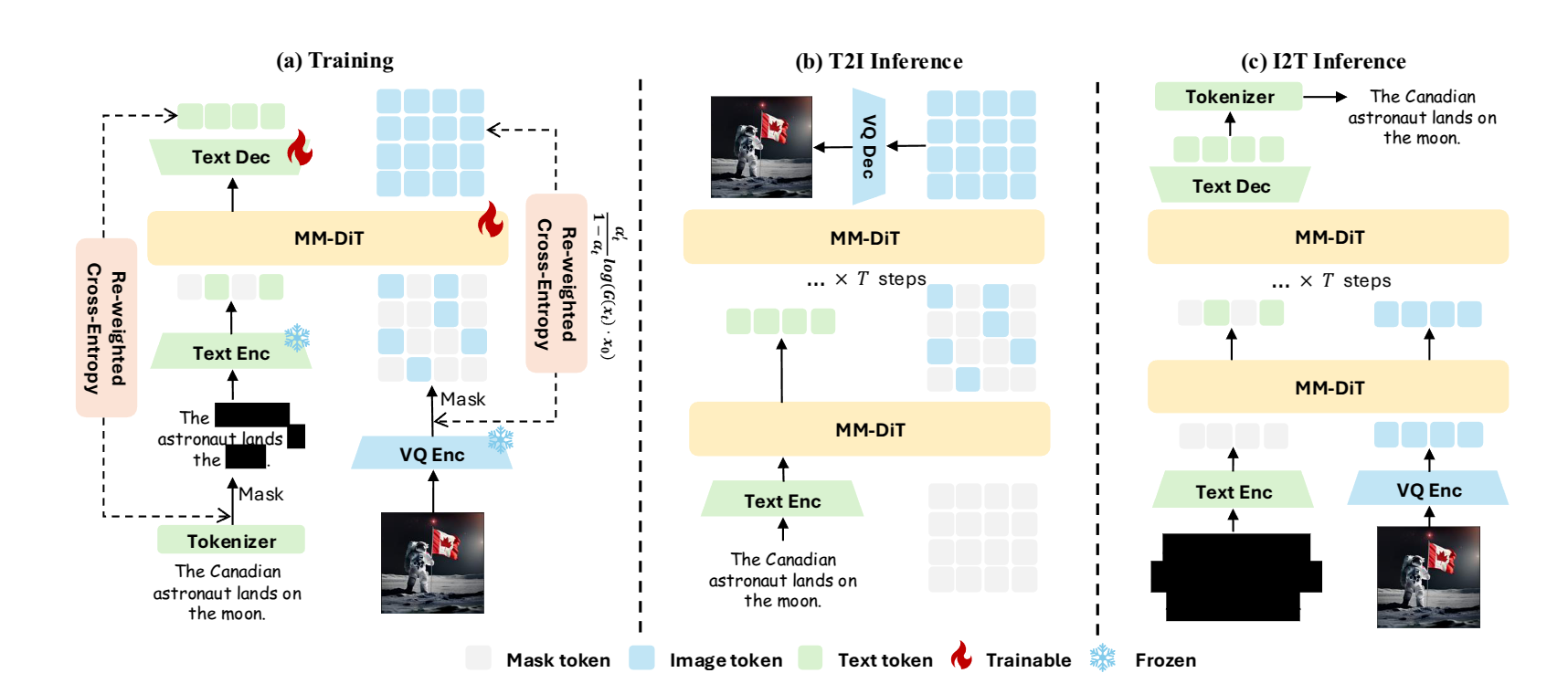
Muddit: Liberating Generation Beyond Text-to-Image with a Unified Discrete Diffusion Model

• Using one unified discrete diffusion for image and text generation

Related Works

• MaskGIT
• Meissonic

Llada Series

• LLADA 1
• LLADA V
• LLADA 1.5

Dual Diffusion for Text-and-Image Generation

Proprietary

• Gemini Diffusion
• GPT-4o

Diffusion-LLM Theory

• A Convergence Theory for Diffusion Language Models: An Information-Theoretic Perspective

Diffusion-LLM Acceleration

• Fast DLLM
  • Two Features:
    1. KV Cache for block-wise decoding
       • It can be used since the activation vector of LLADA-Instruct KV is nearly identical across different block-denoising steps.
       • Dual KV Cache: make following ‘[MASK]’ sequences KV cached when decoding current block
    2. Confidence-Aware Parallel Decoding
       • Why? Curse of parallel decoding, two related tokens may be decoded in parallel, leading to a loss of coherence.
       • How? Compute a confidence score for each token, unmask tokens exceeding a certain threshold. If no tokens exceed the threshold, decode one with highest confidence to avoid deadlock.
       • Why this works? Formal solution: greedy parallel (product of marginal distribution) decoding is equivalent to greedy sequential (true joint distribution) decoding in the high-confidence regime.
       • 
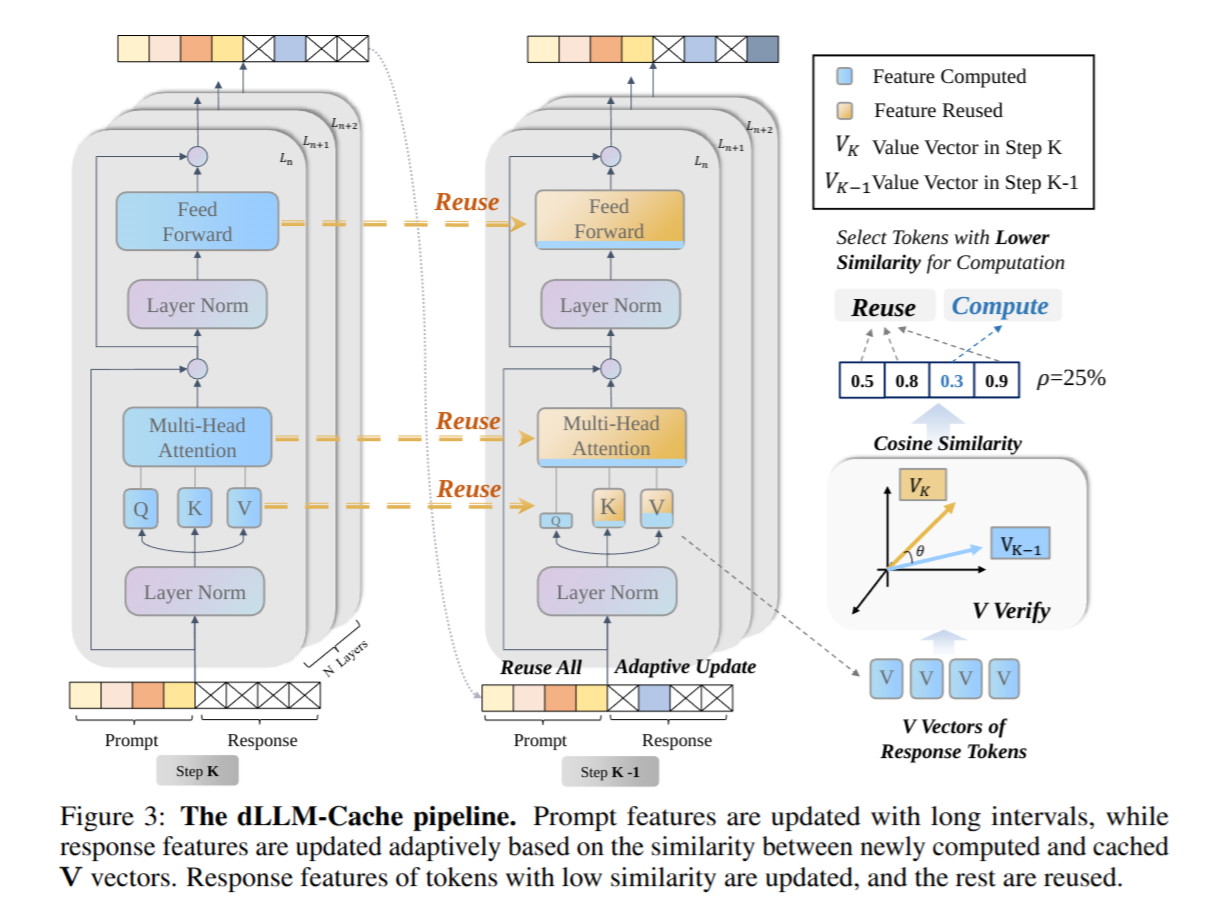
• dLLM-Cache
  • This paper investigate the KV changing mechanism(similar to above)
  • How to identify significantly changing tokens?
    • Exp shows K/V changing is strongly correlated with the changes in its subsequence $\mathbf{AttnOut}$ and $\mathbf{FFNOut}$.
    • Pipeline: